Bienvenido al curso Pro Statistics
Puedes acceder a la versión Premium con tutoriales paso a paso, soporte y asesoramiento
Índice >> Lección 1 >> Lección 2 >> Lección 3 >> Lección 4 >> Lección 5 >> Lección 6 >> Lección 7 >> Lección 8 >> Lección 9 >> Lección 10 >> Lección 11 >> Lección 12 >> Lección 13 >> Tutorial R >> Tutorial Excel >>Tutorial SPSS Errores >> Casos de Éxito >> Opciones para Aprender >> FAQ’s >> Lista de Softwares
¿Cómo interpretar la función de densidad de probabilidad y cómo comprender la más famosa de ellas: la distribución normal?
¡No te asustes!
Sé que la palabra «función» te suena matemático. Puedo escuchar el Errghh en tu cabeza.
Tranquilo que todo tiene su sentido. El lenguaje matemático se inventó para interpretar el mundo objetivamente.
Hoy vas a entender por fin la función de densidad de probabilidad.
Y de rebote entenderás mucho mejor qué es una distribución normal y para qué sirve.
Estamos construyendo las bases del análisis estadístico.
¡A por ello!
¿Qué vas a aprender en la lección de hoy?
- La relación entre el histograma de densidad y la función de densidad de probabilidad
- Qué es y cómo utilizar la distribución normal o Gaussiana
# Del histograma de densidad a la función de densidad de probabilidad
Si recuerdas el histograma de densidad es un histograma especial. El área de las barras es igual a 1.
Eso hace que la altura de las barras no dependa del número de observaciones de la muestra.
Fíjate en estos histogramas.
Son histogramas de menor a mayor muestra. De 100 individuos a 100000 individuos. La altura es la misma ya que son histogramas de densidad.
Y cada vez se intuye mejor el contorno de la distribución.
Sobretodo en el último de ellos.
¿Te imaginas un histograma con barras tan pequeñas que puedas dibujar un contorno perfecto?
Pues precisamente ese contorno es la función de densidad de probabilidad.
Te he preparado un artículo dónde te explico este concepto con más detalle.

# La función de densidad de probabilidad por excelencia: la distribución normal
Ahora que entiendas qué es una distribución de densidad de probabilidad estás más que preparado para comprender la famosa distribución normal. O distribución Gaussiana.
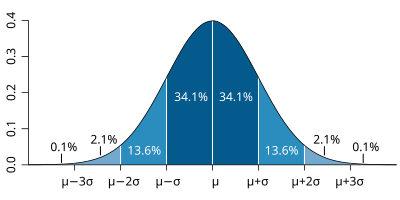
Supongo que has visto este gráfico alguna vez.
Puedo intuir que los porcentajes, las letras mu’s y sigma’s de la imagen no acabas de tenerlo claro. Don’t worry.
Voy a intentar a poner un poco de luz:
- Los porcentajes son probabilidades. Las áreas de debajo la función densidad de probabilidad son, en definitiva, probabilidades.
- La mu es la media de la población. La media o promedio. El valor central.
- Y la sigma es la desviación estándar de la población. La dispersión.
Ahora quiero explicarte cómo de importante es la distribución normal y cómo utilizarla. Te he preparado un artículo y comprenderás todo lo necesario sobre la distribución normal 🙂
…
En la siguiente lección te explicaré qué es el intervalo de confianza y cómo puedes utilizarlo en la práctica.
Yo soy ingeniero. Y los ingenieros no somos nada exactos.
Siempre nos regimos por la regla del más o menos. O margenes de seguridad.
El intervalo de confianza se utiliza en muchas ocasiones pero no todo el mundo entiende su significado.
Tú vas a ser un privilegiado 🙂 Podrás presumir de utilizarlo sin equivocarte 🙂
¡Hasta ahora!
…
ACCEDE A LA FORMACIÓN PREMIUM C2
Training Fast Track Analizar Datos desde cero
Curso Analiza tu Estudio