Seguro que el termino frecuencia te ha llegado alguna vez.
Seguramente has oído que la electricidad de tu casa está a 60 Hz 0 50Hz dependiendo del país. ¿Verdad?
Estos «Hz» son unidades de frecuencia. Hoy vas a salir de aquí sabiendo que significa «frecuencia».
Y además este concepto está muy relacionado en saber interpretar la dinámica de una serie temporal.
La dinámica es cómo va evolucionando tu serie en el tiempo. Cómo se va moviendo durante un período de tiempo.
Y para observar está dinámica vas a utilizar la famosa transformada de Fourier y ¡»su mundo» en la frecuencia!
¿Te atreves a descubrirlo?
¡¡¡AVISO!!! Incluye un ejemplo al final de post
# Una analogía: la crema de verduras
Imagínate un sistema que te permita «desmezclar» lo que tienes.
No sé si existe el verbo «desmezclar». Mejor separar, ¿verdad? 😛
¡Eso es! Un sistema capaz de separar los elementos de algo mezclado. ¡Estarás flipando! jejeje
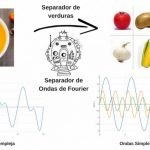
Imagina un sistema que separe las verduras enteras de una crema de verduras. (ya sé que es imposible pero atrévete a imaginarlo)
En una crema de verduras esta todo mezclado. No sabes si comes calabacín, cebolla, patata o que es… Una vez en la boca ya ni lo sabes. El gusto final es la suma de muchos gustos.
¡No te preocupes! Hoy no estás aquí para aprender a separar verduras. Más bien, vas a separar series temporales 🙂
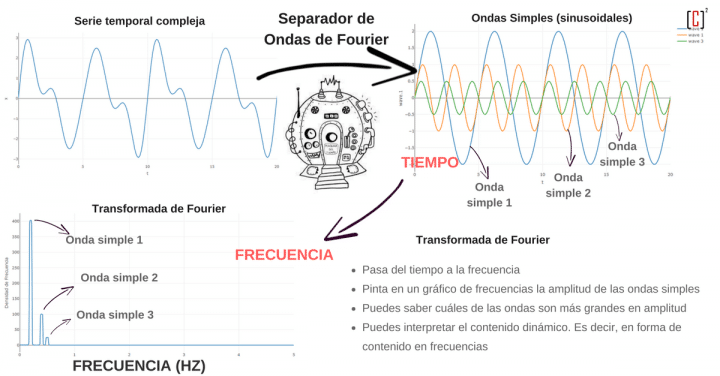
Te presento a La Transformada de Fourier. Un sistema capaz de separar las verduras de la crema de verduras. ¡Es algo extraordinario! ¿No crees?
Mira la imagen:
Imagina que la crema de verduras es una serie temporal compleja.
Y las verduras son ondas con la forma más básica de onda.
Con ello vas a poder pasar de la serie temporal a un espectro en frecuencias para analizar la dinámica de tu serie temporal. ¡Toma!
Este es el objetivo de hoy.
Descubre cómo analizar los datos de tus proyectos con éxito.
Sin perder miles de horas descifrando fórmulas estadísticas incomprensibles.
# Explicando una serie temporal como la suma de muchas ondas
Una serie temporal es, en el fondo, la suma de muchas ondas como las que has visto antes. Estas ondas tienen la forma típica de un sin(x) o cos(x). ¿Te acuerdas?
El señor Fourier demostró que existe este sistema «separador de verduras» (matemáticamente hablando).
Siempre puedes separar una serie temporal como la suma de muchas ondas de dimensiones diferentes y con ritmo también diferentes.
Algo así.
Esto es la transformada de Fourier. Es un separador de series temporales en ondas simples.
Ahora te explico mejor que quiero decir con ondas simples.
# La onda simple o onda sinusoidal
La gracias del sistema separador de ondas de Fourier es que la serie temporal se expresa en forma de ondas muy simples.
Ahora te voy a explicar los tres conceptos más importantes en un onda simple o onda sinusoisal 🙂
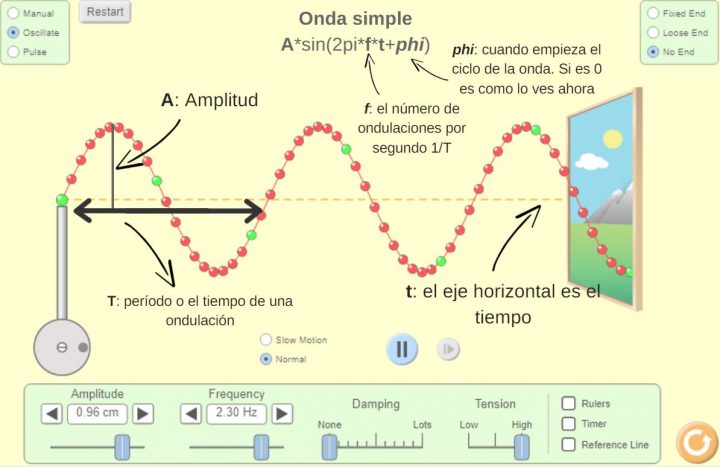
Una onda es bonita y sigue una harmonia muy suave como la que ves en la imagen.
para caracterizar esta onda tienes los siguientes conceptos:
- Amplitud: es lo alta o baja que es
- La frecuencia: es el ritmo que lleva. O es el número de ondulaciones por segundo
- El desfase: es cuando empieza la onda.
Matemáticamente es así:
- A: Amplitud
- f: la frecuencia es el inverso del período (1/T). El período es el tiempo de duración de una ondulación completa.
- fi: el desfase
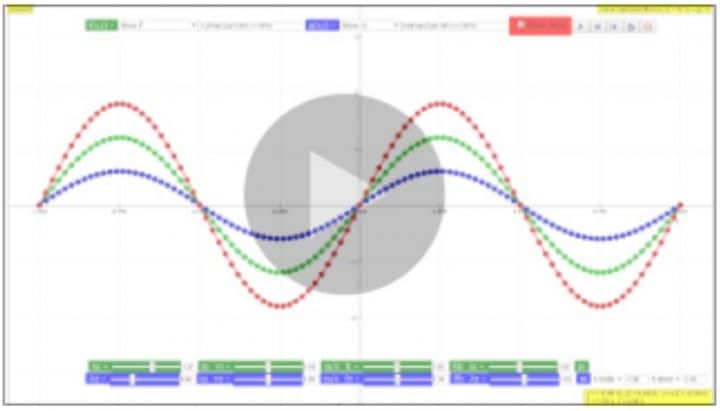
Puedes jugar un poquito en este simulador de 2 ondas y visualizar la suma de las dos:
Hasta aquí bien, ¿verdad?
Has visto el sistema separador de Fourier que es capaz de expresar una serie temporal en la suma de ondas bonitas. Has visto qué características tienen estas ondas bonitas.
Déjame detenerme en el concepto de frecuencia. Es la clave para entender el sistema separador de Fourier 😉 ¡Vamos a ello!
#El concepto de frecuencia
El ejemplo que todo el mundo ha visto: el reloj. Voy a tratar de explicarte que es la frecuencia con la ayuda de las agujas del reloj 😉
- La minutera se mueve cada 60 segundos: 1/60 Hz
- La segundera se mueve cada 1 segundo: 1/1 Hz
- La hora se mueve de posición cada 3600 segundos o cada 60 minutos: 1/3600 Hz
Estos valores son frecuencias. Vueltas o repeteciones dividido por unidad de tiempo (segundos)
Cuanto más baja es la frecuencia más lento es el proceso
Pasa lo mismo con la onda sinusoidal que has visto antes.
Aquí tienes un simulador de ondas. Intenta crear una onda bonita como la que has visto en el punto anterior. Te sugiero que le des a la opción de Oscillate y No End en la parte superior izquierda y derecha respectivamente. Entenderás mucho mejor el concepto de frecuencia:
Por ejemplo la señal eléctrica de 220V que pasa los enchufes de nuestra casas da 60 vueltas cada segundo 60/1. Es de 60 Hz. El valor del voltaje no es constante en el tiempo. Sino que es una onda bonita como la que te he explicado antes. Y por tanto a veces se hace 0.
En realidad la luz de nuestras casas se enciende y se apaga 60 veces por segundo. Va tan rápida que ni la percibimos.
¿Puedes crear una onda sinusoidal de 5V y 60Hz con la ayuda de este simulador. (A mi me ha costado un poquito jejeje)
Estás mucho más preparado para entender el separador de Fourier.
¡Let’s go!
Descubre cómo analizar los datos de tus proyectos con éxito.
Sin perder miles de horas descifrando fórmulas estadísticas incomprensibles.
# El separador de Ondas de Fourier
Repito: el separador de ondas de Fourier es la máquina de «desmezclar» verduras que te comentaba al principio.
Y es capaz de separar una serie temporal super rara en la suma de ondas simples (como las que has visto antes)
Según el separador de ondas que montó Fourier hace ya unos años tenemos esto:
- Mi serie temporal = suma de Ondas Simples
- Mi serie temporal = Sumatorio (A_i * sin(2PI*f_i t + desfase_i))
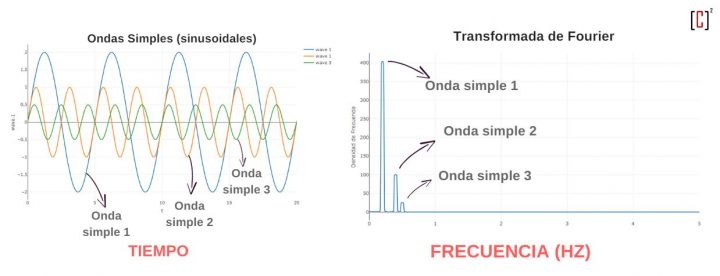
La gracia del separador es que nos permite dibujar las amplitudes de las ondas en función de la frecuencia. ¡Toma!
De esta manera es más fácil visualizar las magnitudes de las ondas (amplitud) y lo rápidas o lentas que van (frecuencia)
Es el llamado mapa de frecuencias o espectro de frecuencias.
¡No te asustes! Es una manera de dibujar las ondas que ha encontrado el separador en un papel. De esta manera será más fácil de interpretar todas estas ondas simples.
# Los dos mundos: el tiempo y la frecuencia
El separador de Fourier es capaz de pintar tu serie temporal que está en el tiempo y la pinta en el mundo del ritmo, de la frecuencia. Por este motivo, se dice que la transformada de Fourier pasa del espacio temporal al espacio frecuencia. (¡suena más cool y complicado!)
¡En este tipo de gráficos queda condensada toda la información de las ondas que has obtenido el separador de Fourier!
Sólo necesitas las amplitudes o A’s y las frecuencias o f’s de las ondas que has encontrado con el separador.
- Podemos pasar de una serie temporal complicada a una suma de ondas.
- Y podemos dibujar esto en un mapa de frecuencias. Utilizando la frecuencia como medida para diferenciar las diferentes ondas.
La gracia de este espectro de frecuencias o mapa de frecuencias es que puedes ver a simple vista el contenido de las ondas resultado de utilizar el separador de ondas de Fourier. Y de esta manera caracterizar la dinámica de la serie temporal.
Una serie temporal la puedes pasar a una gráfico en frecuencia.
Esta es la idea.
Estos gráficos son muy buenos para entender el contenido en frecuencia. Es decir qué ondas son las más grandes y en qué frecuencia van.
# La transformada de Fourier en matemáticas
¡Para los más valientes! Te he preparado una sección sobre cómo se escribe todo esto matemáticamente.
He utilizado una pequeña imagen de esta página dónde se resume toda la notación:
Como sé que te será difícil entenderlo, lo mejor es que consultes a los cracks. Para mi el mejor artículo que jamás he visto sobre la transformada de Fourier y la matemática que hay detrás.
¡Vas a flipar!
>> Accede al artículo de betterexplained.com y ¡flipa!
# Un ejemplo de aplicación
Voy a tratar de explicarte lo que has visto en el post con un pequeño ejemplo.
Este ejemplo consiste en calcular la transformada de Fourier para la serie temporal que has visto en las imágenes del artículo 😉
¡Seguro que lo tendrás más que claro!
¡No te lo pierdas!
…
Descubre cómo analizar los datos de tus proyectos con éxito.
Sin perder miles de horas descifrando fórmulas estadísticas incomprensibles.
En próximos artículos te explicaré más en detalle qué es el espectro de densidad de frecuencias y alguna aplicación real para que entiendas mucho mejor todo lo que has visto hoy 🙂
La transformada de Fourier es un concepto complicado. En este artículo he intentado focalizarte en el objetivo práctico de la transformada más que en explicar la notación matemática.
¿Qué tal si me dices qué tal te ha parecido? ¿Tienes dudas? Te espero en los comentarios 😉
Hola! Mi nombre es Alexandra soy bióloga y me ha parecido muy interesante tu explicación, además de ponerlo en un modo muy sencillo explicas de maravilla. Todo muy claro.
Bienvenida Alejandra! Me alegro tener una bióloga más en el blog 🙂 Gracias por los elogios! Me voy a poner rojo 😉
Muy bien estructurado de manera sencilla para entender el concepto.
Gracias Yris! Nos seguimos viendo por el blog 😉
Jordi… muy bien; y el video de youtube genial con RStudio.
Voy a tratar de sacar las frecuencias propias de un onda de sonido real y te cuento….
Enhorabuena.
Genial! Espero que te salga bien 🙂
Felicidades! muy buen trabajo, mi nombre es Daniel soy Ingeniero Civil y todo el tiempo me relaciono con matemáticas avanzadas y su aplicación.
Que bien Daniel! Gracias! Los expertos como tú aplican las matemáticas en el día a día. Es estructuras la dinámica es fundamental 🙂
Abrazos!
Muy buena explicacion
Gracias Marcos!
Buenas!! He de darte las gracias. En las prácticas externas de la universidad estoy trabajando con un dispositivo. La FFT es uno de los conceptos que necesito manejar y, gracias a este artículo, me están quedando las ideas bastante claras. Agradezco mucho tus aportes, ¡sigue así!
¡Gracias a ti por escribirme :)!
Y a seguir aplicando la fft 🙂
Soy estudiante.
Muy buena explicación, gracias…
Graciaaas 😉
Genial y gracias por la explicación, voy a compartir este post.
Que bien! Gracias a ti!
Hola Jordi, muchas gracias por tu importante contribución al entendimiento de la ciencia. Me gustó mucho tu manera tan divertida de explicar, algo realmente «complejo», jajaja.
Soy Geofísica y para nosotros esto es el pan de cada día en el análisis y comprensión de las señales sísmicas
¡Gracias!
Es un concepto complejo pero lleno de utilidad 🙂
¡Mola!
Muchas gracias por la explicación, estoy en una investigacion del tema aplicado a vibraciones sísmicas y el uso de espectros de respuesta
¡Sí! El mundo en frecuencia es una pasada y muy complicado al inicio.
Espero que con el post te ayude a entenderlo 🙂
Abrazos!
Hola soy estudiante de ingeniería en computación (IPN) y tu explicacion mas el articulo añadido a esta pagina. Me ayudo bastante a entender el concepto de que es la transformada de Fourier y poder darle significado a los conceptos matemáticos que estoy viendo. Además en el articulo añadido pude ver ya aplicaciones donde se puede aplicar este concepto. UNA FELICITACIÓN POR ESTE ARTICULO QUE CREASTE.
https://conceptosclaros.com/transformada-de-fourier/
articulo añadido: https://betterexplained.com/articles/an-interactive-guide-to-the-fourier-transform/
Realmente genial! Poder explicar de manera amena, fácil y divertida un concepto a veces complejo. Muchas Gracias.
Dónde podría encontrar más temas relacionados con señales y sistemas?
Soy estudiante de Ingeniería Mecatrónica y me encantaría saber más del tema o temas relacionado a ingeniería.
De nuevo, gracias.
Hola!. Soy ingeniera civil y tu explicación es genial!!. Quiero dedicarme a la docencia y quisiera poder hacer llegar a mis estudiantes la información de esta manera. Saludos!
Hola mucho gusto, soy profesor de ecuaciones diferenciales y la forma en que explicas los conceptos es una maravilla, nosotros lo aplicamos a señales eléctricas que a final de cuentas es la utilidad mas socorrida
Excelente
Thanks! 😉
Hola, genial tu post, me encantaría que de la misma manera tan clara pudieses explicar por favor las propiedades de la transformada de Fourier que por más artículos que leo y en libros sigo sin entender el concepto de estas propiedades, como la de escalamiento, desplazamiento, etc. felicidades por tan buenos aportes.
Gracias!
Las propiedades de la transformada de Fourier son muy interesantes. Si me animo aclararé sus propiedades ya que son claves para entender los espectros de frecuencia 🙂
Abrazos!
Gracias ñor la informacion, estudio mecatronica y me estan atorando feo con Fourier y me esta costando mucho el entender que es, que hace y como funciona
hola mi nombre es Luis Alberto, me dedico a hacer analisis de ultrasonido por aire para inspecciones de lineas electricas de media tensión, me parecio muy explicatica y sencilla para entender el concepto de transformadas de furrier
Hola paso a felicitarte, soy música y hasta ahora estoy entendiendo los conceptos de sonido. Me gustaría aprender sobre acústica. Un abrazo
Hola disculpa ¿cual es el compilador con el que obtuviste tus gráficas? Por cierto, gracias por tu artículo de verdad es muy útil
Gracias Luis, por tus palabras y por estar por aquí! Un abrazo
Buenas, Dices: «En realidad la luz de nuestras casas se enciende y se apaga 60 veces por segundo.» en realidad lo hace 120 veces y 100 veces cuando son 60 o 50hz respectivamente.
muy bueno el posteo muchas gracias!
clarisimo , yo he llegado aqui para saber la utilidad en la practica en la electronica