Hoy toca hablarte de la recta de regresión. Te voy a enseñar a crear una función matemática para predecir una variable numérica en función de otras. Y me dirás, Jordi, ¿para qué me va a servir?
Bien, me gusta que te preocupes por la utilidad ?
Por ejemplo, quieres predecir (estimar) los partidos que ganarás en la liga en función del número de goles que marques al acabar la temporada.
Otro ejemplo: quieres predecir (estimar) el consumo de un coche sabiendo únicamente su peso.
Quieres encontrar (estimar) la frecuencia cardíaca máxima según la edad, el peso y la altura de los pacientes.
¿Quieres saber cómo responder a este tipo de preguntas? Sigue leyendo y verás qué es la recta de regresión y cómo se utiliza en la práctica.
¡Vamos a ello!
AVISO: el artículo incluye dos tutoriales paso a paso de cómo puedes calcular una recta de regresión en Excel y en R
¿Qué es un modelo lineal de predicción? El concepto que hay detrás de la recta de regresión
Los ejemplos que te he citado en la introducción nacen del impulso del cálculo de un modelo. Y usarlo para la predicción.
Antes de enseñarte qué es la recta de regresión, mejor tener claro qué es un modelo para predecir.
Inconscientemente hacemos estos modelos predictivos en nuestra mente.
Somos tan inteligentes que utilizamos técnicas como la que te explico hoy sin darnos cuenta. Y seguramente mejor calculadas ?
Para hacerlo, el cerebro humano utiliza la experiencia. Almacena una base de datos para después calcular el modelo. Utilizarlo para predecir. Y al final tomar decisiones acertadas. Que es de lo que trata un modelo.
A base de palos y algún que otro suspenso me di cuenta que para aprobar un examen de la universidad podía estudiar de tres formas:
- Echando horas en casa estudiando sólo.
- Ir a todas las clases y hacer las tareas que me sugería el profesor.
- O echando horas practicando con exámenes de años anteriores con otros compañeros.
Por experiencia, (gracias a la base de datos inconsciente que me creé) conseguí ver cuán importantes son estos tres aspectos en el resultado de la nota final de la asignatura.
Y detecté que hacer exámenes de años anteriores me preparaba mucho mejor para el examen que atender a clase o estudiar el temario solo en casa.
¡El peso de la variable “horas practicando exámenes de años anteriores” es muy importante! Es la que más influye.
En este caso me creé inconscientemente un modelo lineal:
Nota en el Examen = a*Horas Estudiando Solo +
b*Horas atendiendo a Clase +
c*Horas resolviendo Exámenes
¡Eso es!
La nota en el examen depende de las horas que dedique a las tres maneras de estudiar. La a la b y la c son el peso de importancia en la nota final del examen. Se llaman coeficientes de modelo de regresión.
Acabas de descubrir qué es un modelo lineal. Y ahora ya sabes la idea principal de la predicción. Te permite entender la realidad con una función matemática. Déjame detallarte un poco más esta idea:
Imagina que tienes recogidos en un Excel diferentes casos de estudiantes donde sabes las horas que ha invertido en cada tipo de estudio y el resultado final del examen.
Con esos datos podríamos calcular la recta de regresión (modelo lineal) y estimar la nota en el examen en función de las horas dedicadas a cada tipo de manera de estudiar.
Al final del artículo vas a ver un ejemplo práctico de cómo calcular la recta de regresión con Excel y con R para que lo puedas probar tú misma.
Descubre cómo analizar los datos de tus proyectos con éxito.
Sin perder miles de horas descifrando fórmulas estadísticas incomprensibles.
La estructura principal de los modelos (que también utiliza la recta de regresión) y los dos súper poderes
Detrás de estos modelos siempre hay una estructura muy clara.
Una estructura de entradas – salida.
O dicho de otra forma, variables explicativas – variable respuesta.
Voy a ponerte otro ejemplo real para ilustrar esta idea:
Queremos estimar la frecuencia cardíaca máxima (que son las pulsaciones del corazón de máximo esfuerzo físico) explicadas por la edad y el sexo de los deportistas.
Dicho de otra forma queremos estimar solo con el sexo y la edad cual sería la frecuencia cardíaca promedio más o menos.
Por ejemplo, ¿qué frecuencia cardíaca máxima le corresponde a una persona que es mujer y tiene 36 años?
¿Se entiende la idea?
Lo que vamos a hacer es estructurar el modelo de esta manera:
¿Se ve?
Entro la edad y sexo como variables de entrada o explicativas, y me va a salir la variable Y que es la frecuencia cardíaca máxima (variable respuesta).
¡Maravilloso!
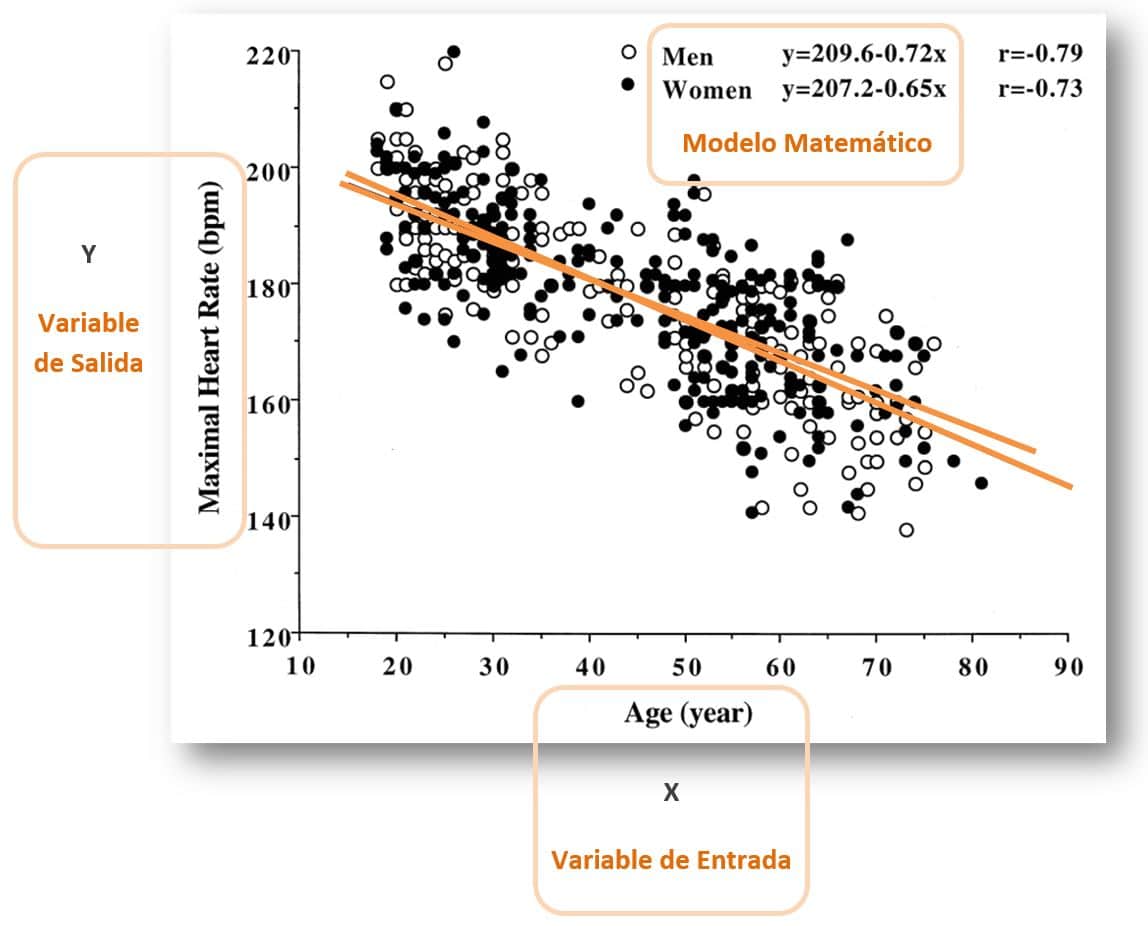
Gráficamente nos queda algo así:
Esta es la esencia de los modelos estadísticos y también de la recta de regresión.
De hecho, en la imagen puedes ver dos rectas de regresión. Una para los hombres y otra para las mujeres. Ambas rectas son modelos lineales de regresión.
Fíjate que estas rectas están pintadas encima de un diagrama de dispersión (nube de puntos) y cada recta explica los puntos blancos o negros según sea la recta de hombres o mujeres respectivamente.
Está recta es el modelo más sencillo posible porque es lineal y nos relaciona una variable Y de salida con una respuesta X de entrada.
Si seguimos con el ejemplo, mirando la imagen podemos definir la ecuación para mujeres:
Frecuencia_Cardíaca_Máxima_Mujer = 207.2 – 0.65*Edad
¡Esto es maravilloso!
Porque te permite predecir la frecuencia cardíaca máxima de las mujeres solo poniendo la edad.
Si la deportista tiene 35 años, entonces, la frecuencia cardíaca máxima es 207.2 – 0.65*35 = 184.45 pulsaciones por minuto.
Además me doy cuenta que si aumento la edad, por ejemplo, 50 años, entonces el valor de pulsaciones baja.
207.2 – 0.65*50 = 174.7 pulsaciones por minuto.
¡Uaahla!
¡Es porque el coeficiente que acompaña la edad es negativo! (-0.35)
¡Y tachán!
Ahora ya sabes los dos súper poderes de los modelos y también de la recta de regresión:
- Qué peso y en qué sentido influyen las variables de entrada a tu variable de salida. Por ejemplo, la edad influye negativamente.
- Puedes usar la recta de regresión (modelo) para predecir o estimar tu variable respuesta.
¡Bien!
Ahora que tienes la idea más clara …
Vamos a por un poco de detalle matemática y un ejemplo práctico.
¡A por ello!
¿Qué es una recta de regresión?
¡Bien!
Ahora ya estás muy preparado para entender qué es una recta de regresión e ir a los detalles.
Y hoy vengo para explicarte el modelo más simple, un modelo lineal. ¿Te acuerdas? Un modelo no es más que una función matemática que calculas gracias a datos que observas. Y después utilizas esta función matemática para predecir nuevos datos. Y hoy te hablo del modelo más sencillo, pero quizá el más fácil de entender.
El análisis de regresión lineal no es más que encontrar un modelo lineal. Una función matemática. La función de una recta. Así de simple.
Es decir, encontrar la mejor función de la recta que te permita predecir el valor de una variable sabiendo los valores de otra variable que observes. ¡Vale! Ya te estoy liando. Aquí un ejemplo para los más futboleros:
Quieres crear un modelo lineal que permita predecir los partidos que ganarás en la liga en función del número de goles que marques en la temporada.
Lo primero es dibujar los puntos en un gráfico. Y después intentar obtener una recta que mejor explique los puntos del gráfico. O dicho de otro modo, que mejor explique el comportamiento de tus datos.
Como te decía, el modelo que buscas en la regresión lineal es una recta. Y como habrás visto en este post, la recta tiene esta pinta:
La regresión trata de calcular a y b que ves en el recuadro azul para construir la recta más coherente con lo datos que tengas.
Pero algo pasa. ¡¡¡Este chico está preocupado!!! ¿Cuál será la recta que mejor explica los datos que tengo? ¿De las líneas de regresión posibles cuál elijo?Puedo dibujar miles. Y todas parecidas. ¿Cuál escojo?
Y la verdad es que es una excelente pregunta. Y la respuesta la tendrás cuando hagas el análisis de regresión simple. Podría acabar el post aquí pero no quiero dejarte con la intriga ?
El análisis de regresión se encarga de dibujar la recta con el error mínimo. ¡Voy al rescate!
Por ejemplo, ¿ves la distancia entre el punto y la recta marcada en rojo? Este es el error del modelo a ese punto observado. O el residuo del modelo a ese punto observado.
Cada punto tiene una distancia a la recta. Y esta distancia es el error de cada punto.
La recta de regresión que busca el niño es la recta que tiene la suma de distancias más pequeña de todas las rectas posibles. Ahora ya sabes qué es la recta de regresión y cómo se calcula.
Resumiendo:
Una recta de regresión es un modelo lineal que relaciona una variable de salida Y con otra variable X.
En un problema de regresión la variable de salida Y tiene que ser cuantitativa. Es medible.
En el caso de que tengas solamente una variable de entrada X, entonces la fórmula de la recta es la siguiente:
Y = a + b*X + error
La anterior fórmula se refiere a una modelo de regresión simple porque solo tenemos una variable de entrada.
Ahora vamos a desgranar cada uno de los valores de la recta:
a y b son coeficientes del modelo de regresión. Son un número.
- a es el valor del cruce de la recta con el eje vertical. Se llama intercept en inglés. Te lo digo así porque es como sale en la mayoría de softwares estadísticos.
- b es la pendiente de la recta. Si b es positiva la relación es positiva y va hacia arriba. Por ejemplo, cuanto más peso tenga un coche más consumo tendrá. En ese caso b será positivo. Otro ejemplo, cuanto mayor es la edad disminuye la frecuencia cardíaca máxima, b en este caso sería negativa.
- X es la variable de entrada. La edad en el ejemplo de la frecuencia cardíaca máxima y goles a favor en el ejemplo de los partidos ganados.
- Error es el residuo. Es el error de predicción de cada punto a la recta. Es decir, es la diferencia entre el valor de tu recta y el valor real u observado.
¡Bien!
¡Ahora ya has avanzado muchísimo!
El siguiente paso es afianzar la utilidad práctica de la recta de regresión.
¿Para qué sirve la recta de regresión?
En la práctica la recta de regresión y otros modelos de regresión tienes dos usos prácticos muy interesantes:
Uso práctico nº1 de la recta de regresión: qué y cómo influyen las variables en la respuesta.
Poder explicar una característica en función de otras variables estadísticas y entender qué variables son las que más influyen y cómo.
Este uso práctico te permitiría contestar a preguntas tipo:
- cómo influyen los hábitos saludables en la presencia o ausencia de hipertensión.
- qué aspectos socioeconómicos son los que afectan a la felicidad de los habitantes de un país y cómo.
- ¿La esperanza de vida tiene que ver con la riqueza de un país? Cómo afecta la riqueza o PIB per cápita a la esperanza de vida promedio.
- ¿Cómo afecta la edad, el estilo de vida, el tipo de trabajo en el burnout o stress laboral?
- ¿La empleabilidad de los alumnos de las universidades se puede explicar por la valoración de la universidad a nivel nacional e internacional, la cantidad de proyectos con empresas que colabora la universidad, la cantidad de publicaciones anuales etc…? ¿Qué aspectos ayudan a las universidades a que sus alumnos tengan un mayor grado de empleabilidad?
- …
- …
¿Se entiende la idea?
¿Podrías añadir algunos ejemplos más?
Al final lo que queremos es cuantificar qué características o variables afectan a una determinada variable de salida que nos interesa estudiar.
Para ello es muy importante plantear y recoger los datos de las características de entrada y la característica de salida.
Una vez tengas la tabla de datos ya es momento de aplicar la recta de regresión en el software estadístico como vas a ver en el siguiente apartado.
Vamos a poner un ejemplo muy simple:
Los puntos de la imagen representan modelos de coche. Algunos son más pesados o menos pesados son el eje horizontal.
Nota: en la imagen puedes ver el coeficiente de correlación lineal R que es de 0.89 que nos indica que tenemos una relación positiva y muy cercana a 1 que es el máximo de correlación lineal. De hecho la correlación y regresión no son lo mismo. La correlación cuantifica la relación y la regresión crea el modelo causal entradas-salida.
Y en el eje vertical tienes el consumo. Esta es tu variable respuesta.
Este modelo te está diciendo que cuanto aumenta el peso, aumenta el consumo.
Esta es la salida de la recta de regresión del software estadístico cuando calcula la ecuación de la recta de ajuste. Fíjate:
En amarillo tienes los coeficientes:
El intercept = 0.006169
El coeficiente que acompaña el Peso es 0.014938
Entonces la recta de regresión es:
Consumo = 0.006169 + 0.014938*Peso + Error
Si te fijas en la imagen, en una flechita roja puedes ver la significación estadística de la variable Peso.
Si tienes asteriscos, significa que tienes significación estadística y la primera variable Peso influyen en la variable Consumo.
Esta es la conclusión.
Pero vamos a complicar un poco la cosa.
Imagínate que en lugar de solo poner el peso pongo otras variables como los caballos del motor.
Mira que sucede con el modelo:
Ahora quedaría la fórmula del modelo de regresión así:
Consumo = 6.305e-03 + 1.149e-02*Peso + 7.479e-05*Caballos + Error
Las dos variable son significativas, es más evidente el peso ya que Pr (>|t|) o p-valor es más pequeño en el caso del peso que en los caballos.
Las dos variables tienen un coeficiente positivo. Influyen positivamente en el consumo.
Si quisieras interpretar un poco mejor el modelo podrías pintar para diferentes Caballos la recta consumo vs peso por ejemplo.
Este es un modelo de regresión lineal múltiple ya que usamos dos variables de entrada en lugar de una como el ejemplo anterior.
Cuando hablamos de recta de regresión es porque solo usamos una variable de entrada y podemos dibujar esa recta en plano 2D.
Espero que hayas comprendido la esencia de la primera utilidad de la recta de regresión y, en general, de los modelos de regresión lineales.
Descubre cómo analizar los datos de tus proyectos con éxito.
Sin perder miles de horas descifrando fórmulas estadísticas incomprensibles.
Uso práctico nº2 de la recta de regresión: la predicción de la variable de salida.
Ya has visto que la recta de regresión nos permite explicar una determinada variable de salida, y, en función de una variable de entrada x.
De aquí no sale la famosa fórmula: y = a+bx
Eso es, una regresión de x. Esta fórmula se obtiene de un conjunto de datos que hemos recogido durante pruebas a diferentes deportistas. Fíjate que ambas variables son numéricas.
En la imagen puedes ver la nube puntos de la base de datos. Cada punto representa a un deportista dónde se sabe su edad,x, y también sabemos el la frecuencia cardíaca máxima, y que se obtiene de una prueba de esfuerzo.
La recta de regresión es un compromiso entre todos los puntos que hemos observado. Es el centro de gravedad, el equilibrio en la relación que explica la y en función de la x.
Y de eso trata las rectas de regresión de poder explicar la variable y en función de la x basados en datos obtenidos a priori.
Esta recta nos permite predecir o estimar que frecuencia cardíaca máxima te corresponde.
Prueba tu con estas fórmulas:
- Para hombres: FCM_hombres = 209.6-0.72*Edad
- Para mujeres: FCM_mujeres = 207.2-0.65*Edad
Prueba con poner tu edad y calcula la estimación de tu Frecuencia Cardíaca Máxima.
Ese es el segundo uso práctico.
Una vez tenemos el modelo, la recta de regresión, la podemos usar para estimar que valores corresponden con nuevos casos sin necesidad de hacer la prueba de esfuerzo de la FCM.
¿Cómo hacer una regresión en Excel? Tutorial con vídeo
Ahora que ya entiendas qué es una recta de regresión y para qué sirve la recta de regresión es momento de pasar a la práctica.
En este primer tutorial del artículo vas a trabajar con Excel. Excel te permite calcular la recta de regresión sin ningún problema usando su modelo de Análisis de Datos o agregando la línea de tendencia a un diagrama de dispersión.
Ya verás que es muy sencillo y estoy seguro que a partir de ahora ya lo usarás en la práctica 🙂
Vamos a seguir con el ejemplo que tenemos de la FCM y la edad y de esta manera lo veremos muy claro y fácil. Descarga el ejemplo, mira el vídeo y a practicar:
DESCARGA LOS DATOS Y EJEMPLO DE CÓMO CALCULAR LA RECTA DE REGRESIÓN EN EXCEL
¡A por ello!
En el vídeo te explico dos maneras de calcular la recta de regresión en Excel:
Manera 1. Agregar línea de tendencia a par tir del gráfico de dispersión:
- Crea un gráfico de dispersión con Excel y después agrega la línea de tendencia en el gráfico:
- Selecciona los puntos del gráfico de dispersión y botón derecho encima de ellos. Te aparecerá esta opción:
Manera 2. Utiliza la opción regresión del módulo de análisis de datos de Excel:
- Activa el módulo de análisis de datos en Excel.
- Ves a la pestaña Datos – Análisis de Datos. Te aparecerá esta opción:
Mira el vídeo que te he preparado y te será muy fácil.
La ventaja de calcular la recta de regresión de la manera 2 a través de la herramienta de análisis de datos es que te calcula los estadísticos relacionados con la recta de regresión y los residuos:
Bien, ahora que sabes cómo calcular la recta de regresión es momento de hacerlo con un software estadístico muy potente: R.
¡Sigue leyendo y te explico cómo hacerlo!
Descubre cómo analizar los datos de tus proyectos con éxito.
Sin perder miles de horas descifrando fórmulas estadísticas incomprensibles.
¿Cómo hacer una regresión en R? Tutorial con vídeo
Excel no es un software estadístico como tal aunque te permita calcular la recta de regresión de forma fácil.
En esta sección te quiero explicar cómo calcularla con un software estadístico gratuito y que funciona realmente bien aunque necesitas usar la programación: R Software.
Lo primero y más importante es instalar R y RStudio en tu ordenador.
Si ya lo tienes instalado ya puedes empezar con el tutorial. Para ello te he preparado el código de R y también los datos para que puedas hacer el ejercicio.
DESCARGA EL CÓDIGO Y DATOS DE CÓMO CALCULAR LA RECTA DE REGRESIÓN EN R
¡Vamos con el tutorial paso a paso!
Sigue los pasos que te marco en el vídeo y ya tienes todo el material para calcular tu recta de regresión en R siempre que quieras 🙂
¡Espero que lo utilices en tus datos!
—
Espero que este artículo te haya ayudado a entender qué es una recta de regresión, para qué sirve y cómo se calcula la recta de regresión en Excel y R.
De hecho los modelos de regresión son técnicas muy utilizadas en el análisis de datos y una de las más potentes.
En el training de estadística gratuito vas a entender mucho mejor las distintas técnicas estadísticas que existen y su utilidad para acabar entendiendo un proceso para analizar los datos de forma segura.
